Iowa Measurement and Research Foundation

Submitted by
Dae S. Hong (Danny), Assistant Professor
Department of Teaching and Learning
Mathematics Education Program

Project Title: Measuring Quality of Instruction in Calculus Lessons

The purpose of this project is to measure quality of current instructional practices of calculus classes and examine students’ learning opportunities when they are in calculus classes to identify class-based areas in need of improvement for calculus instructors and students to engage in cognitively challenging mathematical activities. Here are the research questions that we attempted to answer.

1. Do students have opportunities to engage in implemented calculus tasks that challenge them cognitively?
2. Do students have opportunities to experience novel discussions through discourse (or dialog) when working on tasks implemented in calculus lessons?

Methods

Setting and Data

A Midwestern research university in the United States was the setting for this study. Two calculus instructors, Dr. A and Dr. B, have a PhD in mathematics with a specialization in topology and differential geometry, respectively. They have taught Calculus I several times and each class had 25 registered students. Classes were 50 to 55 minutes long and all calculus classes taught by the two mathematicians were videotaped. The sources of data came from class video and audio recordings. In this study, we examined 20 videotaped lessons, 10 from each mathematician.

Cognitive Demand and Task Features

The method used in this study was taken from Stein and her colleagues (1996). In this method, mathematics problems are called mathematical tasks, which are defined as a set of problems or a single complex problem that focuses students’ attention on a particular mathematical idea (Doyle, 1983). Based on Doyle’s definition, we found 103 and 39 implemented tasks from Dr. A and Dr. B’s lessons, respectively. Low cognitive demands are memorization, algorithms, and procedures. High cognitive demands are procedures with concepts, requiring explaining, and reasoning. Table 1 displays examples of low and high level tasks. The first task only requires the procedure of dividing all terms by x^2.  Students can perform this procedure without knowing the meaning behind the procedure, a characteristic of a low-level task. The second task was coded as high level, procedure with connection, because the task requires more than the procedure of dividing by a term or factoring. Students need to know the range of sine function and properties of parabola.

Table 1:Cognitive Demand by Code

Cognitive Demand	Example
Low
High

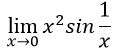
Class-based Influencing Factors

There are several class-based factors that influence cognitive levels during the discussion of each implemented task.

Table 2: Factors Associated with Cognitive Demand

(Adopted from Henningsen & Stein, 1997)

For students to engage with cognitively challenging mathematical activities, the teacher not only needs to select challenging tasks but also implement those tasks in ways that maintain cognitive demands. Hence, we examined class discussion of each task to determine how these factors influenced cognitive levels.

Mathematical Questions Asked during Discussion of Implemented Tasks

Both mathematicians asked mathematical questions. These questions are important parts of class practices because they can sustain pressure for explanations and promote higher level mathematical thinking or they can routinized the tasks and seek only correct answers (Boston & Smith, 2009). We used two terms from the literature ─ novel and routine. Mesa and her colleagues (2014) used the term routine for questions that students know how to procedurally figure out the answer using information given in the class and novel for questions that students are required to explain new and old connections between mathematical notions. Table 3 illustrates an example of each. “What’s the limit as x goes to zero of positive x squared?” was asked when they discussed the task. The question only requires students to have a simple short answer of zero. It does not require explanations or reasoning. The second question was asked when the Intermediate Value Theorem was introduced. The question asks why a continuous function needs to cross x-axis if the function has both positive and negative values. The question requires students to think about the concept of continuous functions.

Table 3: Instructors’ Questions by Code

Instructional Quality Assessment

Using MTF as the foundation, Boston (2012) developed ways to measure the quality of mathematical instruction, called the instructional quality assessment (IQA) (Boston, 2012). IQA was designed to provide statistical and descriptive data about the nature of instruction and students’ opportunities to learn (Boston, 2012). There are important observable indicators of high quality mathematical instruction: 1) implementation of cognitively challenging instructional tasks, 2) opportunities for students to participate in high–level thinking and reasoning, and 3) opportunities for students to explain their mathematical thinking and reasoning (Boston, 2012). For this study, we used the IQA of three Academic Rigor rubric (Boston et al., 2015): Potential of the Task, Task Implementation, and Rigor of Teachers’ Questions. Potential of the Task identifies the highest level of thinking and explanation that the written task has the potential to elicit from students. Task Implementation measures the highest level of thinking in which the majority of students actually engaged during the discussion of each task. Third, Rigor of Teachers’ Questions assesses types of reasoning required by teachers’ questions during the discussions of each task. Each of these three indicators can be scored from 0 to 4 (with 0 indicating absence of the measure). The procedure for analysis of the discourse and tasks consisted of segmenting the transcript by each mathematical tasks discussed and conducting a line-by-line coding of the dialogue, as well as scoring all class discussions and implemented tasks by the level of engagement and cognitive demands as the rubrics indicated (Boston, 2012). Measuring these three important aspects of mathematical instruction will help us identify areas in need of improvement and give specific feedback to calculus instructors to directly influence calculus students’ opportunities to learn.

Coding Procedures and Reliability

From set–up to implementation, all 142 mathematical tasks and class discussions for these tasks were coded by the author and two graduate students. We paid attention to cognitive demand, task features and factors that maintain cognitive demand during class discussions. Since some of these factors occurred at the same time during the discussion of a mathematical task, there are several cases where we used several codes. When two coders did not agree, we followed majority rule. In all, the percent agreement of the three raters for cognitive demand and task features was between 93% and 96%. For class discussions, it was between 90% and 93%.

Results

Cognitive Demand

The cognitive demand of implemented tasks shows that the majority of these tasks (95.1 % and 100 % from Dr. A and Dr. B’s classes respectively) requires low level cognitive demand. This means that students only had limited opportunities to engage in cognitively demanding tasks.

 Table 4 Percent distribution of implemented tasks by cognitive demand

Mathematical Questions asked During the Discussions

In addition to overall low cognitive demand, opportunities for students to participate in high-level thinking were rare. Table 5 details the types of mathematical questions asked during task implementation.  Questions were frequently routine mathematical questions, such as “What is the antiderivative of this function?” or “Is the area positive or negative?” However, occasionally novel questions were presented, pressing for further explanations from students (e.g. “How did you know that?”) or requesting reasoning for the next step in a process (e.g. “What should we do next? How do you know?”). Furthermore, in many cases, the types of mathematical questions used during tasks limited the discussion that followed. While Dr. A asked frequent questions, she would only obtain more than two students’ answers on average 30% of the time. In Dr. B’s class, answers were always limited to one or two students. In all cases, student answers to both routine and novel questions were very brief; discussion would end when a correct answer was provided.

Table 5 Percent distribution Mathematical Questions Asked.

Influencing Factors Associated with Cognitive Demand

Three most notable influencing factors that declined cognitive demand in Dr. A’s lessons are no waiting time (63.1 % - 65 times out of 103 implemented tasks), and routinized tasks by taking over the discussions (64 %). The influencing factors that maintained cognitive demand during Dr. A’s lessons are waiting time (36.9 %) and use of student’s prior knowledge (7.8 %) were two notable factors. Sustained pressure for explanations and scaffolding almost did not occur (1.3 %). In all, there was one time during the ten lessons that Dr. A and her students were able to maintain cognitive demand or make connections between procedures and concepts. The influencing factors that reduced cognitive demand during Dr. B’s ten lessons are no waiting time (97.4 % - 38 out of 39 tasks) and routinized tasks (97.4 %). In Dr. B’s lessons, influencing factors to maintain cognitive demand such as use of student’s prior knowledge scaffolding students’ thinking, sustained pressure for explanations, and monitoring students,’ did not occur – there was only one waiting time. For all 39 calculus tasks, Dr. B and his students were not able to maintain cognitive demand or make connections between procedures and concepts. They mainly talked about the procedures of solving calculus problems.

Table 6 Influencing factors that associated with cognitive demand[1]

IQA Rubrics

Putting these results together, we used IQA rubrics to rate all twenty lessons. Tables 7 and 8 show the average scores for each lesson using three IQA rubrics. The average for these rubric scores again confirm that tasks were mostly about procedures and algorithms (rating of 2 means tasks require procedures and algorithms) and questions required only short responses (rating of 1 means the teacher asks procedural or factual questions that elicit mathematical facts or procedure or require brief, single word responses), which indicate the needs of implementing more cognitively demanding tasks and asking more novel questions so that students can be pressured to explain their thinking.

Table 7 Dr. A – IQA Rubrics

Table 8 Dr. B – IQA Rubrics

Discussion and Conclusion

In this study, we examined 20 calculus lessons to understand students’ opportunities to learn cognitively challenging tasks and maintain cognitive demand during calculus lessons. Since our results are based directly on day-to-day instructional practices, we hope our results will have more widespread impact in the actual teaching of calculus. We acknowledge that it will be a challenging and time-consuming process to change calculus instructors’ instructional practices, but providing class-based individualized feedback is a step toward reforming instructional practices. The results of this study may or may not be surprising. In one sense, we confirmed that lecture is still main mode of teaching in Calculus 1. On the other hand, we did not expect that over 90% of tasks were at a low level. With our findings, the real question is, “How can we use these results to improve calculus teaching?” One way is to collaborate with mathematicians to share our findings so they can reflect on their teaching. With our findings, we can suggest the following for Dr. A and Dr. B. For Dr. A, more mathematical questions that require explanations and reasoning are needed because over 70 % of her questions only required simple and short answers. These questions often sought only correct answers. In addition, instead of taking over the discussion, Dr. A needs to give her students opportunities to reflect and monitor their work. For Dr. B, it is critical to ask more questions, give them time to think about tasks, and provide students opportunities to explain and monitor their thinking. Dr. B tended to lecture and explain everything and, as a result, his students worked on only a few tasks and were asked only a handful of mathematical questions. Furthermore, even if many tasks required only low-level cognitive demand, both Dr. A and Dr. B should attempt to use students’ prior knowledge to assess understanding so that students have opportunities to make connections between procedures and concepts.

References

Bergsten, C. (2007). Investigating quality of undergraduate mathematics lectures. Mathematics Education Research Journal, 19(3), 48-72.

Bezuidenhout, J. (2001). Limits and continuity: Some conceptions of first-year students. International Journal of Mathematical Education in Science and Technology, 32(4), 487–500.

Blanton, M., Stylianou, D. A. & David, M. M. (2003). The nature of scaffolding in undergraduate students' transition to mathematical proof. In the Proceedings of the 27^th Annual Meeting for the International Group for the Psychology of Mathematics Education. (vol. 2, pp. 113-120), Honolulu, Hawaii.

Boston, M. D. & Smith, M. S. (2009). Transforming secondary mathematics teaching: Increasing the cognitive demands of instructional tasks used in teachers' classrooms. Journal for Research in Mathematics Education, 40(2), 119-156.

Boston, M. (2012). Assessing instructional quality in mathematics. The Elementary School Journal, 113(1), 76–104.

Bressoud, D. M. (2011). The worst way to teach. Retrieved 27 March, 2013, from http://www.maa.org

Bressoud, D., Burn, H., Hsu, E., Mesa, W., Rasmussen, C., & White, N. (2014). Successful calculus programs: Two-year colleges to research universities. Paper presented at the meeting of the National Council of Teachers of Mathematics, New Orleans.

Doyle, W. (1983). Academic work. Review of Educational Research, 53(2), 159-199.

Ellis J., Kelton, M., & Rasmussen, C. (2014). Student perceptions of pedagogy and associated persistence in calculus. ZDM, 46(4), 661–673.

Henningsen, M., & Stein, M. K. (1997). Mathematical tasks and student cognition: Classroom-based factors that support and inhibit high-level mathematical thinking and reasoning. Journal for Research in Mathematics Education, 28, 524−549.

Hourigan, M., & O'Donoghue, J. (2007). Mathematical under-preparedness: The influence of the pre-tertiary mathematics experience on students' ability to make a successful transition to tertiary level mathematics courses in Ireland. International Journal of Mathematics Education in Science and Technology, 38(4), 461–476.

Mesa, V., Celis, S., & Lande, E. (2014). "Teaching approaches of community college mathematics faculty: Do they relate to classroom practices?" American Educational Research Journal. 52, 117-151.

Nardi, E. (2008). Amongst Mathematicians: Teaching and learning mathematics at university level. USA: Springer.

Pritchard, D. (2010). Where learning starts? A framework for thinking about lectures in university mathematics. International Journal of Mathematical Education in Science and Technology, 41(5), 609–623.

Rasmussen, C., Marrongelle, K., & Borba, M. (2014). Research on calculus: What do we know and where do we need to go? ZDM – The International Journal on Mathematics Education, 46(4), 507-515.

Seymour, E., & Hewitt, N. M. (1997). Talking about leaving: Why undergraduate leave the sciences. Boulder, CO: Westview Press.

Tall, D., & Vinner, S. (1981). Concept image and concept definition in mathematics, with particular reference to limits and continuity. Educational Studies in Mathematics, 12, 151–169.

Several products have resulted from this project, including:

CONFERENCE PROCEEDINGS

 Hong, D., & Choi, K. (2015). WHAT IS HAPPENING IN CALCULUS 1 CLASSES? THE STORY OF TWO MATHEMATICIANS. Bartell, T. G., Bieda, K. N., Putnam, R. T., Bradfield, K., & Dominguez, H. (Eds.). (2015). Proceedings of the 37th annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education. East Lansing, MI: Michigan State University.

 CONFERENCE PRESENTATIONS

Hong, D. (2016, July). Maintaining Cognitive Demand During Limit Lessons: A Challenging Class Practice. Paper to be presented at the 13th Meeting of International Congress on Mathematics Education, Hamburg, Germany.

Hong, D. & Choi, K. (2016, July). What is the Current State of Calculus 1 Classes?: The Results from Two Calculus 1 Classes. Paper to be presented at the 13th Meeting of International Congress on Mathematics Education, Hamburg, Germany.

Hwang, J., Hong, D., & Choi, K. (2016, July). Use of Instructional Examples in Calculus Classrooms. Paper to be presented at the 13th Meeting of International Congress on Mathematics Education, Hamburg, Germany.

Hwang, J., & Hong, D. (2015, November). Use of Examples in Teaching Calculus: Focus on Continuity. Poster presented at the 37th Annual Conference of the North American Chapter of the International Group for the Psychology of Mathematics Education (PME-NA 2015), East Lansing, Michigan .

Hong, D., & Choi, K. (2015, November). What is happening in Calculus 1 classes? : the story of two mathematicians. Paper presented at the 37th Annual Conference of the North American Chapter of the International Group for the Psychology of Mathematics Education (PME-NA 2015), East Lansing, Michigan .

 Manuscripts under review

 Hong, D. Maintaining Cognitive Demand During Limit Lessons: A Challenging Class Practice. Mathematics Education Research Journal (under review)